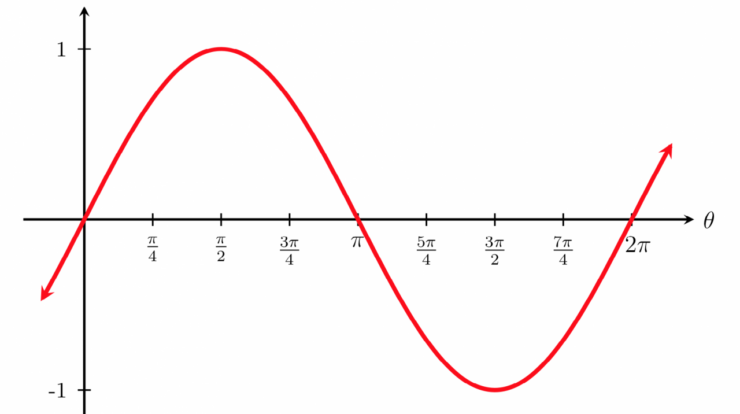
At the heart of trigonometry lies a concept that unravels the secrets of angles and shapes: sine. This trigonometric function holds a profound significance, extending its influence across a diverse range of disciplines, from physics to music. Embark on an enlightening journey as we delve into the sine meaning, tracing its historical evolution, exploring its applications, and uncovering its mathematical essence.
In this comprehensive guide, we will unravel the intricacies of sine, examining its role in defining the unit circle, understanding the interplay between sine, cosine, and tangent, and harnessing its power to solve trigonometric equations.
Sine in Mathematics: Sine Meaning
Sine is a trigonometric function that describes the vertical component of a right triangle. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
Mathematical Definition of Sine
The sine of an angle θ is defined as:
sin(θ) = opposite/hypotenuse
where opposite is the length of the side opposite to the angle θ and hypotenuse is the length of the side opposite to the right angle.
The range of the sine function is [-1, 1]. The sine function is periodic with a period of 2π.
Applications of Sine in Real-World Scenarios, Sine meaning
Sine is used in a variety of applications in physics, engineering, and music.
In physics, sine is used to describe simple harmonic motion. Simple harmonic motion is a type of periodic motion that occurs when an object is attached to a spring or other elastic object.
In engineering, sine is used to analyze the vibrations of structures. Sine waves are also used in sound waves and acoustics.
Historical Evolution of Sine
The concept of sine was first developed by ancient Greek mathematicians. Hipparchus of Nicaea (c. 190 – c. 120 BC) developed a table of chords that included the values of sine for different angles.
Ptolemy (c. 90 – c. 168 AD) expanded on Hipparchus’s work and developed a more accurate table of sines.
The sine function was further developed by Indian mathematicians in the 5th century AD. Aryabhata (476 – 550 AD) developed a formula for calculating the sine of an angle.
Sine in Trigonometry
Sine is one of the three basic trigonometric functions. The other two trigonometric functions are cosine and tangent.
The sine, cosine, and tangent functions are related by the following identities:
sin2(θ) + cos 2(θ) = 1tan(θ) = sin(θ)/cos(θ)
Sine in Calculus
The derivative of the sine function is the cosine function:
d/dx sin(x) = cos(x)
The integral of the sine function is the negative cosine function:
∫ sin(x) dx =
cos(x) + C
Outcome Summary
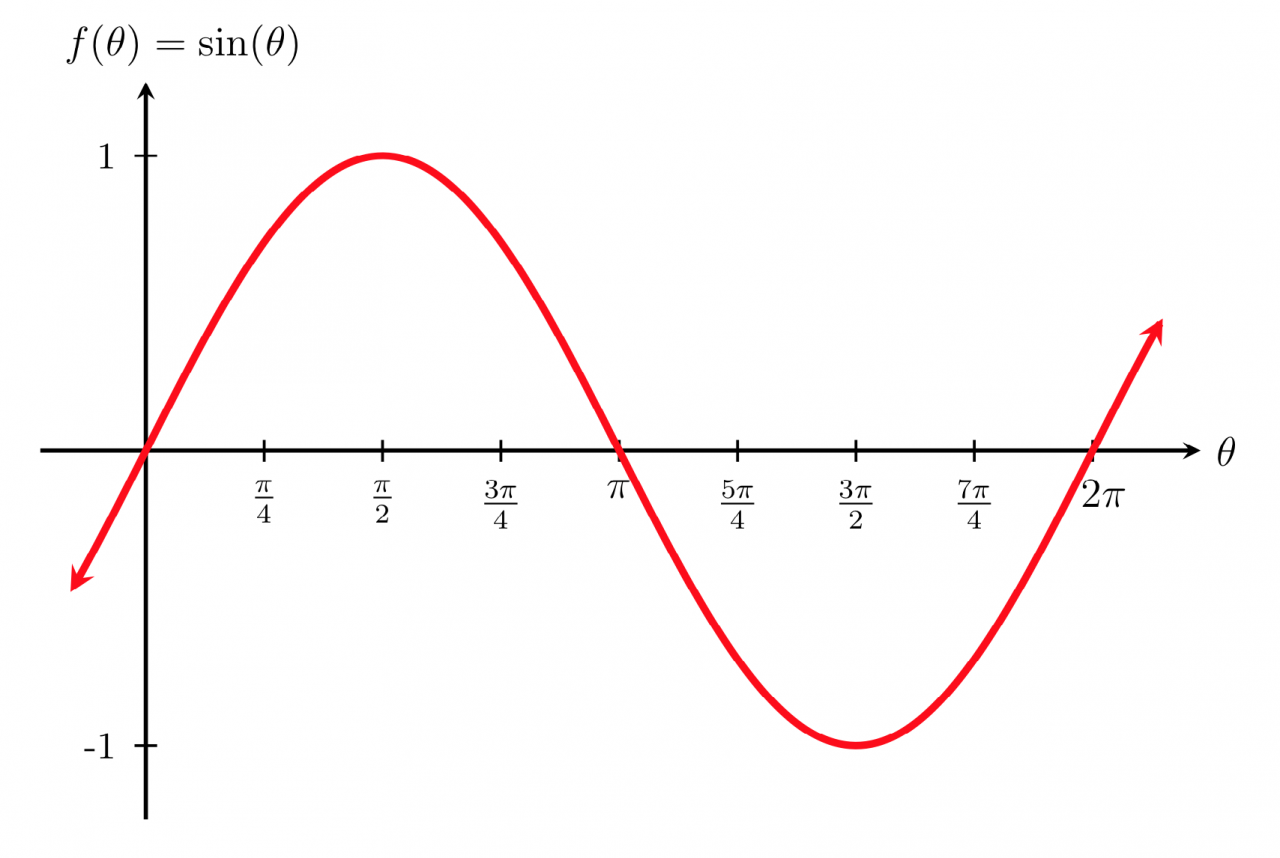
As we conclude our exploration of sine meaning, it is evident that this trigonometric function transcends mere mathematical abstraction. Its applications span a vast array of fields, shaping our understanding of the world around us. From the rhythmic oscillations of sound waves to the intricate trajectories of celestial bodies, sine plays an indispensable role in unraveling the complexities of our universe.
Questions Often Asked
What is the mathematical definition of sine?
Sine is a trigonometric function that represents the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse.
How is sine used in real-world scenarios?
Sine finds applications in physics, engineering, and music. It is used to calculate the trajectory of projectiles, design bridges, and analyze sound waves.
What is the historical evolution of sine?
The concept of sine has been traced back to ancient civilizations, with significant contributions from mathematicians like Hipparchus and Ptolemy.